'잡동사니'에 해당되는 글 13995건
- 2024.11.01 워크샾 컴백
- 2024.10.31 워크샾
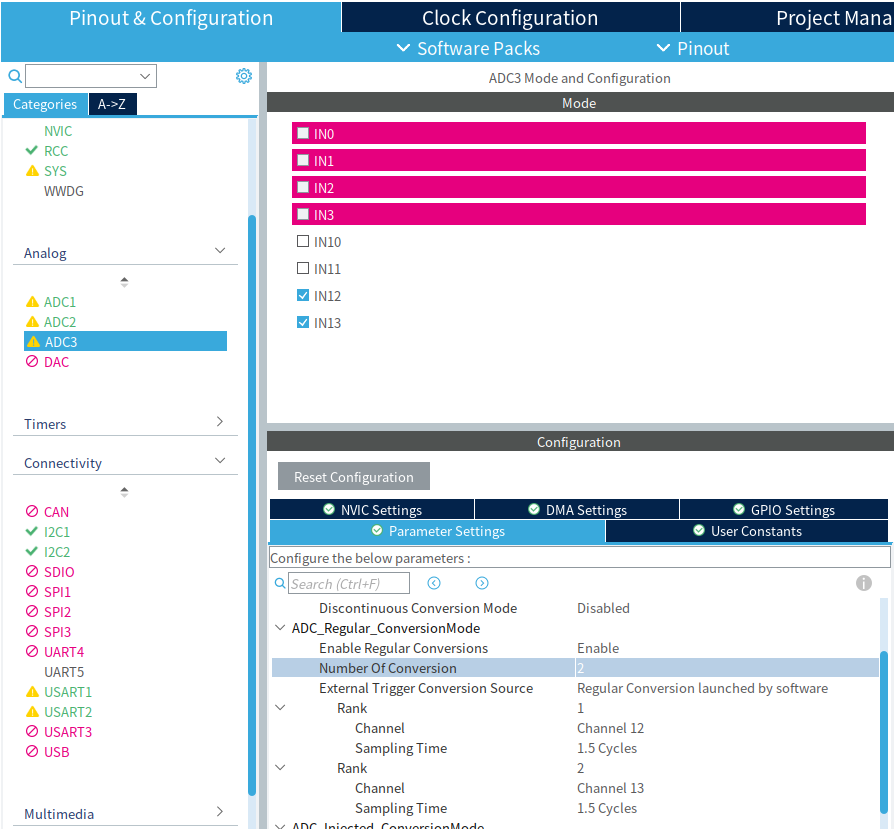
- 2024.10.30 stm32 adc 읽기(1개로 여러 개 채널)
- 2024.10.29 일이 치이는 중
- 2024.10.28 게임 지름 + 선물 강요
- 2024.10.28 SFX-100
- 2024.10.27 f1 (게임) motion data packet 1
- 2024.10.27 daemon x machina 100% side goal 완료! 6
- 2024.10.26 갑분 혈관나이 6
- 2024.10.26 grid 2 motion port
ADC는 3개인데
읽을 핀은 4개라서 어떻게 해야 하나
[링크 : https://m.blog.naver.com/gauya/220232257331]
[링크 : https://github.com/sweesineng/STM32_ADC_MultiCh_SingleConv_Polling?tab=readme-ov-file]
'embeded > Cortex-M3 STM' 카테고리의 다른 글
| stm32 gpio ext interrupt 모드 (0) | 2024.11.04 |
|---|---|
| stm32f103 adc + dma (0) | 2024.11.04 |
| stm32 tim output compare(OC) mode (0) | 2024.07.12 |
| stm32 reset 없이 JTAG 붙이기 (0) | 2023.07.19 |
| STM32H/STM32G 시리즈 시리얼 포트 데이터 order (0) | 2022.08.29 |
DiRT Rally 2.0 는 선물 받고

Forza Horizon 4는 내돈으로 지름
그나저나 카드 쓰면 문자 안왔던가..? 안오네?!

할지도 모르는 게임만 2개 추가!(모든 DLC 포함)
그나저나 용량이 후덜덜하네..
이거 하려면 저번에 얻은 800기가 짜리 SSD로 갈아타야 겠다.. 지금은 256GB 라서 이거 설치 실패할지도..
 |
 |
'게임 > 오리진&스팀&유플레이' 카테고리의 다른 글
| 블랙 프라이데이 할인... 흐음.. (0) | 2024.12.01 |
|---|---|
| 오늘의 게임 다운로드 (0) | 2024.11.02 |
| 갑자기 게임을 지르고 싶어짐 (2) | 2024.10.25 |
| 식물대 좀비 fatal error (0) | 2023.07.23 |
| 오리진 계정 복구 (0) | 2023.06.08 |
3축 시뮬레이터 자작내용을 따라가다 보니 opensfx 의 sfx-100 라는 모델을 발견
SFX-100
정확하게는 액츄에이터 의 모델명이고
[링크 : https://m.blog.naver.com/ilovent/221997600895]
[링크 : https://www.rowanhick.com/sfx-100-build-and-running-guide]
[링크 : https://opensfx.com/]
ac servo driver는 90ST-M02430 이다.
| AC servo motor * | type 90ST-M02430 220V 750W | 4 | Aliexpress | https://de.aliexpress.com/store/product/90ST-M02430-220-v-750-watt-AC-Servo-motor-3000-rpm-2-4-N-M-0/3223052_32844070107.html |
[링크 : https://opensfx.com/shopping-list-and-sourcing-parts/#shopping]
-------------
ac servo driver는 몇가지 모델이 보이는데 동일한 걸려나?
ASD-B2-0721-B
[링크 : https://www.damencnc.com/en/ac-servo-drive-750w-asd-b2-0721-b/a806]
[링크 : https://www.overtake.gg/threads/sfx-100-questions.190790/page-3]
60st-m01330
[링크 : https://www.overtake.gg/threads/al-06-error-on-60st-m01330.209527/]
[링크 : https://ko.aliexpress.com/i/32992008543.html]
90ST-M02430 / 대충 1축당 30만?
[링크 : https://ko.aliexpress.com/item/32844070107.html?spm=a2g0s.9042311.0.0.54484c4d7kuXnA]
opensfx 에서는 aasd 모델의 사용자 설명서를 링크해둔거 보면 asd-b2가 맞는것 같기도 하고?
[링크 : https://opensfx.com/testing-and-configuring-servo-drives/]
'모종의 음모 > motion simulator' 카테고리의 다른 글
| grid 2 핸들 설정 실패 (0) | 2024.11.03 |
|---|---|
| forza horizon 4 - UDP telemetry (2) | 2024.11.03 |
| f1 (게임) motion data packet (1) | 2024.10.27 |
| grid 2 motion port (0) | 2024.10.26 |
| FFBchecker + Driving Force GT (2) | 2024.10.22 |
패킷을 뜯어 보고, 개별 변수가 어떤 의미를 지니는지 검색
f1 게임이긴한데.. codemasters 에서 만들면 비슷하지 않을까 생각중인데..
저번에 udp로 덤프 뜬거랑은 패킷 구조가 맞는지 조차 모르겠어서 나중에 천천히 f1 2015 라도 깔아서 해봐야 할 듯.
모션 패킷에는
월드 좌표계에서의 위치/가속도/방향
중력가속도 횡/종/수직 <<
차량의 yaw/pitch/roll <<
정보로 구성된다.
| struct CarMotionData { float m_worldPositionX; // World space X position float m_worldPositionY; // World space Y position float m_worldPositionZ; // World space Z position float m_worldVelocityX; // Velocity in world space X float m_worldVelocityY; // Velocity in world space Y float m_worldVelocityZ; // Velocity in world space Z int16 m_worldForwardDirX; // World space forward X direction (normalised) int16 m_worldForwardDirY; // World space forward Y direction (normalised) int16 m_worldForwardDirZ; // World space forward Z direction (normalised) int16 m_worldRightDirX; // World space right X direction (normalised) int16 m_worldRightDirY; // World space right Y direction (normalised) int16 m_worldRightDirZ; // World space right Z direction (normalised) float m_gForceLateral; // Lateral G-Force component float m_gForceLongitudinal; // Longitudinal G-Force component float m_gForceVertical; // Vertical G-Force component float m_yaw; // Yaw angle in radians float m_pitch; // Pitch angle in radians float m_roll; // Roll angle in radians }; struct PacketMotionData { PacketHeader m_header; // Header CarMotionData m_carMotionData[22]; // Data for all cars on track // Extra player car ONLY data float m_suspensionPosition[4]; // Note: All wheel arrays have the following order: float m_suspensionVelocity[4]; // RL, RR, FL, FR float m_suspensionAcceleration[4]; // RL, RR, FL, FR float m_wheelSpeed[4]; // Speed of each wheel float m_wheelSlip[4]; // Slip ratio for each wheel float m_localVelocityX; // Velocity in local space float m_localVelocityY; // Velocity in local space float m_localVelocityZ; // Velocity in local space float m_angularVelocityX; // Angular velocity x-component float m_angularVelocityY; // Angular velocity y-component float m_angularVelocityZ; // Angular velocity z-component float m_angularAccelerationX; // Angular velocity x-component float m_angularAccelerationY; // Angular velocity y-component float m_angularAccelerationZ; // Angular velocity z-component float m_frontWheelsAngle; // Current front wheels angle in radians }; |
lateral은 횡이고 longitudinal은 종 인듯 한데
| Unopposed acceleration due to mechanical forces, and consequentially g-force, is experienced whenever anyone rides in a vehicle because it always causes a proper acceleration, and (in the absence of gravity) also always a coordinate acceleration (where velocity changes). Whenever the vehicle changes either direction or speed, the occupants feel lateral (side to side) or longitudinal (forward and backwards) forces produced by the mechanical push of their seats. |
[링크 : https://en.wikipedia.org/wiki/G-force]
[링크 : https://www.mrwaynesclass.com/circular/index08.html]
사전적으로는 아래처럼 정의 되어 있다는데
1. 가로지르기 보단 길이 방향으로 달리기,
2. longitude(경도)에 관련된
음.. 어찌된게 1번이랑 2번이 상반된 내용 같지?
| lon·gi·tu·di·nal /ˌlônjəˈto͞odənl,ˌlänjəˈto͞odənl/ adjective adjective: longitudinal 1. running lengthwise rather than across. "longitudinal muscles" 2. relating to longitude; measured from east to west. "longitudinal positions" 3. (of research or data) involving information about an individual or group gathered over a period of time. "a longitudinal study of ten patients" |
그리고 대망(?)의 yaw / pitch / roll
비행기에서 많이 보던거긴한데 자동차도 이동방향에 대해서는 3개 축에 대한 회전값이 존재할 수 있으니까 머..
yaw는 핸들 돌리면 발생할 것이고
pitch는 길이 오르거나 내리면서 상승 하강 하면 발생할 것이고
roll은 길이 좌우로 기울으면 삐딱하게 가면서 발생할 것이네
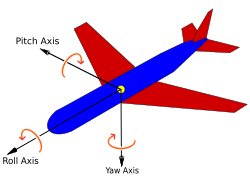
[링크 : https://en.wikipedia.org/wiki/Aircraft_principal_axes]
'모종의 음모 > motion simulator' 카테고리의 다른 글
| forza horizon 4 - UDP telemetry (2) | 2024.11.03 |
|---|---|
| SFX-100 (0) | 2024.10.28 |
| grid 2 motion port (0) | 2024.10.26 |
| FFBchecker + Driving Force GT (2) | 2024.10.22 |
| codemaster telemetry (5) | 2024.10.22 |
일단은 미션 완료!
거의 일주일 걸려서 못하다 빡쳐서(!) 유튜브 찾아봄

범위 공격이 생각외로 넓어서 굳이 많이 이동하지 말고 후딱 잡으면 되었다는게 포인트였는데
그냥 냅다 달려서 때리고 있으니 될리가..
[링크 : https://www.youtube.com/watch?v=_jEriWukvDc]
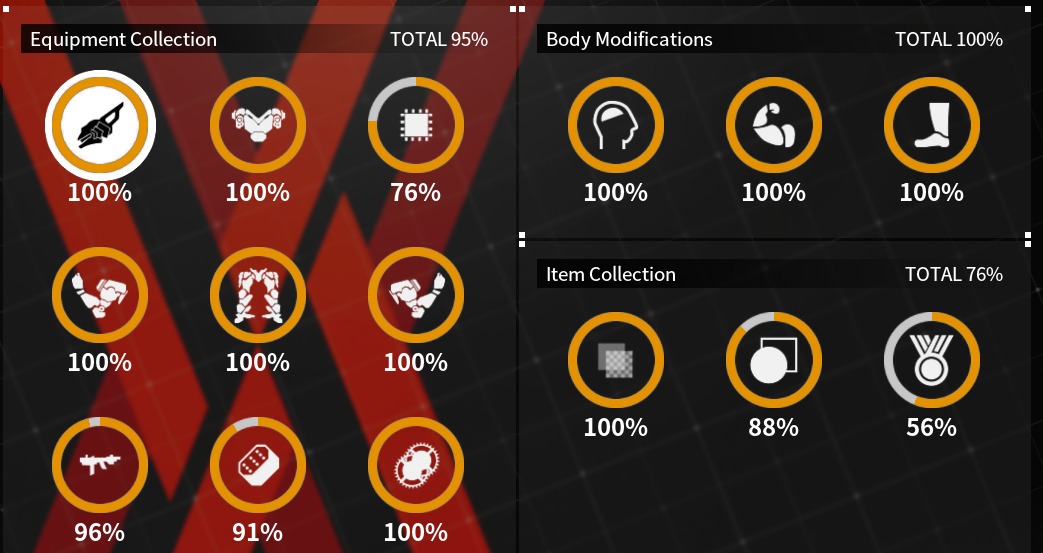
cpu는 왜 76%냐.. 13개 다 모았는데!
무기와 장비 조금 남았고 업적을 좀 끝낼수 있으려나..
'게임 > daemon X machina' 카테고리의 다른 글
| daemon x machina 삭제 (0) | 2025.01.26 |
|---|---|
| 게임삭제 (0) | 2024.05.15 |
| 게임 달려 (0) | 2023.12.31 |
| daemon x machina head 장비 교체 (0) | 2023.11.19 |
| daemon x machina - dainsleif 획득 (0) | 2023.11.04 |
저번에 건강검진에서 가족력도 있고 그래서
동맥 초음파 검사 했는데
70세.. 끄앙..
의사 : 70이면 나쁘진 않아요. 다른분은 120도 나왔어요
아니.. 하나도 위로가 안되는데요.. -_ㅠ
코로나와 육아로 인해서 라고 하면 다들 핑계라고 하겠지만
게다가 출퇴근 거리 편도 2시간이라..
정말 운동할 시간도 없고
지치기만 해서 멀 할수가 없는데.
멀 어떻게 포기해야 건강해질수 있는걸까..
grid 2도 simtools 에서 지원한다고 하길래 포트를 찾아보는데 잘 안보이는 것 같아서 헤매다가
검색해보니 음.. 이걸 해줘야 나오나?
| Apply the change below to your hardware config xml file in ..\Documents\My Games\Grid 2\hardwaresettings\ directory <motion enabled="true" ip="127.0.0.1" port="20777" delay="1" extradata="3" /> </hardware_settings_config> |
[링크 : https://www.eksimracing.org/f-a-q/how-to-get-codemasters-grid-2-working-with-latest-slimax-mgr/]
motion_platform 엘리먼트는 없는디.. 그냥 motion을 udp로 바꾸어도 되려나?
| Open the hardware_settings_config.xml file located in <user>\Documents\My Games\GRID (2019)\hardwaresettings\ with a text editior. Search for the field with the word <motion_platform>. Set the "udp enabled" parameter to "true" and change the "ip" and "port" fields to match that of what was set on the supported telemetry software. For example, <udp enabled="true" extradata="3" ip="127.0.0.1" port="20777" delay="1" /> If user have the D-Box haptic/motion platforms, set the "dbox enabled" parameter to "true". Save the file. |
[링크 : https://www.pcgamingwiki.com/wiki/GRID_(2019)]
d-box 는 d-box technology 회사의 제품이다. 영화관 등에도 사용하는 듯.
[링크 : https://www.d-box.com/en]
[링크 : https://ko.wikipedia.org/wiki/D-BOX]
grid 2의 hardware_settings_config.xml
| <?xml version="1.0" encoding="UTF-8" ?> <hardware_settings_config version="11" deviceId="0x1C03"> <cpu> <threadStrategy workerMapFile="system/workerMap4Core.xml" forceFeedbackProcessor="3" dvdStorageProcessor="3" dataSetMonitorProcessor="1" renderProcessor="0" updateProcessor="2" fileStreamProcessor="3" parallelUpdateRender="true" /> </cpu> <audio_card> <dynamic_range value="high" /> <eq value="flat" /> <voice_chat enabled="true" /> <push_to_talk enabled="false" /> </audio_card> <graphics_card firstBoot="true"> <directx forcedx10="false" /> <eyefinity force="" osd="" /> <stereo enabled="false" separation="0.015" convergence="0.5" /> <advanced forward="false" global_illumination="false" /> <intel tree_aoit="false" particle_avsm="false" particle_aoit="false" /> <resolution width="800" height="600" aspect="auto" fullscreen="false" vsync="0" multisampling="4xmsaa"> <refreshRate rate="60" /> </resolution> <gamma level="0.8" /> </graphics_card> <shadows enabled="true" size="2048" maskQuality="1" particles="true" /> <advanced_fog enabled="true" /> <particles enabled="true" wind="true" dynamicRes="false" lowResScalar="4" /> <crowd enabled="true" detail="2" /> <cloth enabled="true" tessellation="true" /> <postprocess quality="2" /> <groundcover mode="blended" clutter="true" /> <objects lod="1.25" maxlod="0" /> <trees lod="1.25" maxlod="0" /> <vehicles characterQuality="2" lodQuality="2" hires_ai_livery="1" /> <envmap faces="6" size="256" drawallobjects="false" scaleminsize="1.0" mindistance="0.0" /> <water update="true" detail="1" scale="8" tessellation="true" /> <skidmarks enabled="true" /> <dynamic_ambient_occ enabled="true" quality="1" /> <dynamic_ambient_occ_soft enabled="false" /> <night_lighting volumes="true" lights="0" shadows="true" /> <anisotropic min="1" max="8" /> <physics environmentalDamage="true" vehicleDamage="true" /> <input device_type="auto" /> <motion enabled="true" ip="dbox" port="20777" delay="1" extradata="0" /> <screenshotMode enabled="false" /> </hardware_settings_config> |
dirt showdown의 hardware_settings_config.xml
| <?xml version="1.0" encoding="UTF-8" ?> <hardware_settings_config version="62" deviceId="0x1D01"> <cpu> <threadStrategy workerMapFile="system/workerMap4Core.xml" forceFeedbackProcessor="3" dvdStorageProcessor="3" dataSetMonitorProcessor="1" renderProcessor="0" updateProcessor="2" fileStreamProcessor="3" /> </cpu> <audio_card> <audio mixing="rapture3D" /> </audio_card> <graphics_card> <directx forcedx10="false" /> <eyefinity force="" osd="" /> <stereo enabled="false" separation="0.015" convergence="1.5" /> <advanced forward="false" global_illumination="false" /> <resolution width="3840" height="2160" aspect="auto" fullscreen="true" vsync="1" multisampling="4xmsaa"> <refreshRate rate="30" /> </resolution> <gamma level="1.0" /> </graphics_card> <shadows enabled="true" size="1024" maskQuality="1" /> <particles enabled="true" wind="true" dynamicRes="true" /> <crowd enabled="true" detail="1" /> <cloth enabled="true" tessellation="true" /> <postprocess quality="1" /> <groundcover mode="blended" clutter="true" /> <objects lod="1.0" maxlod="0" /> <trees lod="1.0" maxlod="0" /> <vehicles characterQuality="1" lodQuality="1" /> <envmap faces="6" size="256" drawallobjects="false" /> <water update="true" detail="1" tessellation="true" /> <skidmarks enabled="true" /> <dynamic_ambient_occ enabled="true" quality="1" /> <night_lighting volumes="true" lights="0" shadows="false" /> <physics environmentalDamage="true" vehicleDamage="true" /> <input device_type="auto" /> <motion enabled="true" ip="dbox" port="20777" delay="1" extradata="0" /> </hardware_settings_config> |
+
분위기를 보아하니.. 게임프로그램이 server가 아니라 client 인가?
| f1 2010/2011/2012/2013/2014 / grid 2 / dirt 2 / dirt3 </motion enabled="true" extradata="3" delay="1" port="20777" ip="127.0.0.1"> f1 2015/2016 <motion> <udp0 enabled="true" ip="127.0.0.1" port="20777" /> </motion> dirt rally 2.0 / dirt rally </udp enabled="false" extradata="0" ip="127.0.0.1" port="20777" delay="1" > |
[링크 : https://joyqi.com/DashPi]
[링크 : https://support.thrustmaster.com/ko/kb/1786-ko/]
리눅스에서 20777 UDP 포트로 열어 보니 잘 들어 온다.
| $ nc -ul 20777 | hexdump 0000000 f9d1 4181 5d91 4153 e640 43ab 967e 3d9e 0000010 6650 44d0 8c6d c338 8005 439f b318 4097 0000020 ec93 3d8b e4fb bff8 556c c08a 6023 bf7f 0000030 c167 3d0e ba1e 3d77 82dc 3d86 705e 3e33 0000040 7a39 3f7b c898 418b cceb c20d 0255 c0b8 0000050 2a7f c24d 0d02 4500 a511 c29c d300 c419 0000060 1345 41f8 cdf7 41d5 fe46 4243 c4ec c06a 0000070 90a8 4210 0000 0000 0000 0000 0000 0000 0000080 0000 0000 0000 4000 bb8b 3e9f 2ca2 3faf 0000090 0000 0000 2952 4428 0000 3f80 0000 40a0 00000a0 0000 0000 0000 0000 0000 0000 0000 0000 * 00000c0 0000 0000 0000 0000 0000 0000 0000 41a0 00000d0 0000 41a0 0000 41a0 0000 41a0 0000 0000 00000e0 0000 0000 0000 0000 0000 0000 0000 0000 00000f0 0000 3f80 be7b 458a 0000 0000 4274 4437 0000100 622b 42e6 0000 4080 034f 4182 708c 4153 0000110 ea04 43ab 99f8 3d9e 6653 44d0 8ebb c338 0000120 7d79 439f d700 4095 8970 3db3 6bb0 bff8 0000130 5599 c088 282a bf7f dce7 3caf 264e 3da0 0000140 8834 3da5 880f 3e3d b972 3f7a 8afa 41db 0000150 7218 c20f c567 c109 bd32 c24c 07b7 450b 0000160 ef84 c298 5eca c413 cc0f 421c 4f33 41c6 0000170 4f70 4248 c4ec c06a 90a8 4210 0000 0000 0000180 0000 0000 0000 0000 0000 0000 0000 4000 0000190 34ee 3ea1 a017 3fb2 0000 0000 77be 4426 00001a0 0000 3f80 0000 40a0 0000 0000 0000 0000 00001b0 0000 0000 0000 0000 0000 0000 0000 0000 * 00001d0 0000 0000 0000 41a0 0000 41a0 0000 41a0 00001e0 0000 41a0 0000 0000 0000 0000 0000 0000 00001f0 0000 0000 0000 0000 0000 3f80 be7b 458a 0000200 0000 0000 4274 4437 622b 42e6 0000 4080 0000210 0d41 4182 8470 4153 edca 43ab 9d73 3d9e 0000220 6657 44d0 9127 c338 7ad3 439f 2751 4096 0000230 9a99 3db9 5bee bffa 74b5 c088 c99c bf7e 0000240 2646 3beb 8b26 3dc6 9432 3dc5 1cc0 3e48 0000250 d8ad 3f79 4979 4208 7d99 c211 f9df c135 0000260 4462 c24c 9a31 4365 b02c c2cd b34e c3fd 0000270 8ddd 41c4 4156 41ca 228e 4249 c4ec c06a 0000280 90a8 4210 0000 0000 0000 0000 0000 0000 0000290 0000 0000 0000 4000 3c16 3d93 1f67 be09 00002a0 0000 0000 347d 4425 0000 3f80 0000 40a0 00002b0 0000 0000 0000 0000 0000 0000 0000 0000 * 00002d0 0000 0000 0000 0000 0000 0000 0000 41a0 00002e0 0000 41a0 0000 41a0 0000 41a0 0000 0000 00002f0 0000 0000 0000 0000 0000 0000 0000 0000 0000300 0000 3f80 be7b 458a 0000 0000 4274 4437 0000310 622b 42e6 0000 4080 1781 4182 98ef 4153 0000320 f180 43ab a0df 3d9e 665b 44d0 93ae c338 0000330 7819 439f 1e49 4096 2354 3dc7 54e1 bffe 0000340 f3cd c087 40e9 bf7e da0c bbf8 4e57 3dee 0000350 0182 3de6 25dc 3e53 d7da 3f78 1350 4207 0000360 a7d6 c213 17e1 c15d 3e3d c24c 0257 c36a 0000370 1e47 c2b7 f999 c3da 3dc1 c0ee 7e7f 41c6 0000380 539a 4249 c4ec c06a 90a8 4210 0000 0000 0000390 0000 0000 0000 0000 0000 0000 0000 4000 00003a0 9947 3dbb 0eae 3e49 0000 0000 cad3 4424 00003b0 0000 3f80 0000 40a0 0000 0000 0000 0000 00003c0 0000 0000 0000 0000 0000 0000 0000 0000 * 00003e0 0000 0000 0000 41a0 0000 41a0 0000 41a0 00003f0 0000 41a0 0000 0000 0000 0000 0000 0000 0000400 0000 0000 0000 0000 0000 3f80 be7b 458a 0000410 0000 0000 4274 4437 622b 42e6 0000 4080 0000420 222b 4182 ae42 4153 f52c 43ab a443 3d9e 0000430 665f 44d0 965a c338 7546 439f d2ba 4095 0000440 f37c 3ddb 5b0b c001 198b c087 8806 bf7d 0000450 27f4 bcbc e6fc 3e0b 839b 3e03 cd6c 3e5e 0000460 b1bb 3f77 06b6 4203 a9d9 c215 54bb c180 0000470 aca0 c24c 3241 c332 e7eb c2a4 6515 c3c2 0000480 9a57 c144 8d58 41c0 6e0b 424a c4ec c06a 0000490 90a8 4210 0000 0000 0000 0000 0000 0000 00004a0 0000 0000 0000 4000 1c0b 3de2 e01e 3ec4 00004b0 0000 0000 0e13 4424 0000 3f80 0000 40a0 00004c0 0000 0000 0000 0000 0000 0000 0000 0000 * 00004e0 0000 0000 0000 0000 0000 0000 0000 41a0 00004f0 0000 41a0 0000 41a0 0000 41a0 0000 0000 0000500 0000 0000 0000 0000 0000 0000 0000 0000 0000510 0000 3f80 be7b 458a 0000 0000 4274 4437 0000520 622b 42e6 0000 4080 2d34 4182 c453 4153 0000530 f8be 43ab a78e 3d9e 6664 44d0 992a c338 0000540 725f 439f 779f 4095 ca21 3df3 7a1e c003 0000550 2e34 c086 9a44 bf7c 55c7 bd1f 6e7c 3e21 0000560 32dc 3e14 09b2 3e6b 6531 3f76 5897 41ff 0000570 9920 c217 e3bc c190 2524 c24d f5dd c314 0000580 508c c29a 20a2 c3b0 d7ac c128 1fdf 41ba 0000590 c9fa 424b c4ec c06a 90a8 4210 0000 0000 00005a0 0000 0000 0000 0000 0000 0000 0000 4000 00005b0 9441 3ddb 752d 3ed2 0000 0000 2820 4423 00005c0 0000 3f80 0000 40a0 0000 0000 0000 0000 00005d0 0000 0000 0000 0000 0000 0000 0000 0000 * 00005f0 0000 0000 0000 41a0 0000 41a0 0000 41a0 0000600 0000 41a0 0000 0000 0000 0000 0000 0000 0000610 0000 0000 0000 0000 0000 3f80 be7b 458a 0000620 0000 0000 4274 4437 622b 42e6 0000 4080 0000630 3807 4182 d9fa 4153 fc06 43ab aa95 3d9e 0000640 6669 44d0 9bf7 c338 6f8b 439f 0c6c 4095 0000650 ed46 3e06 6b3a c005 384a c085 8287 bf7b 0000660 7269 bd5f 97a1 3e36 269d 3e24 34d3 3e77 0000670 03e6 3f75 195c 41fa 6555 c219 b85e c19f 0000680 90c2 c24d fad7 c2e5 741a c292 9c76 c3a1 0000690 be0f c10a 41ab 41b3 55bc 424d c4ec c06a 00006a0 90a8 4210 0000 0000 0000 0000 0000 0000 00006b0 0000 0000 0000 4000 08e4 3dd9 7db0 3ee7 00006c0 0000 0000 3315 4422 0000 3f80 0000 40a0 00006d0 0000 0000 0000 0000 0000 0000 0000 0000 * 00006f0 0000 0000 0000 0000 0000 0000 0000 41a0 0000700 0000 41a0 0000 41a0 0000 41a0 0000 0000 0000710 0000 0000 0000 0000 0000 0000 0000 0000 0000720 0000 3f80 be7b 458a 0000 0000 4274 4437 0000730 622b 42e6 0000 4080 4319 4182 f01e 4153 0000740 ff2a 43ab ad7a 3d9e 666f 44d0 9ede c338 0000750 6cad 439f 654c 4094 3e0a 3e18 21f4 c007 0000760 0927 c084 3441 bf7a a00f bd90 3d0c 3e4c 0000770 fe88 3e33 e73d 3e81 8015 3f73 c676 41f6 0000780 1fea c21b c281 c1ad f1e3 c24d cce4 c277 0000790 ee42 c286 214a c396 cfa0 c0b0 3649 41aa 00007a0 602b 424f c4ec c06a 90a8 4210 0000 0000 00007b0 0000 0000 0000 0000 0000 0000 0000 4000 00007c0 1db3 3e0c 7b75 3f17 0000 0000 24cd 4421 00007d0 0000 3f80 0000 40a0 0000 0000 0000 0000 00007e0 0000 0000 0000 0000 0000 0000 0000 0000 * 0000800 0000 0000 0000 41a0 0000 41a0 0000 41a0 0000810 0000 41a0 0000 0000 0000 0000 0000 0000 0000820 0000 0000 0000 0000 0000 3f80 be7b 458a 0000830 0000 0000 4274 4437 622b 42e6 0000 4080 0000840 4e42 4182 066f 4154 021a 43ac b030 3d9e 0000850 6676 44d0 a1d4 c338 69d0 439f 79dd 4093 0000860 c6c9 3e1d 2d53 c008 b966 c082 b0f4 bf78 0000870 fe22 bdb1 0c8b 3e62 7515 3e43 53f0 3e88 0000880 df2c 3f71 84d2 41f6 bfb0 c21c fd19 c1ba 0000890 4118 c24e cb3f 4190 aa99 c279 0453 c38d 00008a0 56f1 bfc8 9fa1 419f f57f 4251 c4ec c06a 00008b0 90a8 4210 0000 0000 0000 0000 0000 0000 00008c0 0000 0000 0000 4000 d203 bdc7 9306 3f29 00008d0 0000 0000 e975 441f 0000 3f80 0000 40a0 00008e0 0000 0000 0000 0000 0000 0000 0000 0000 * 0000900 0000 0000 0000 0000 0000 0000 0000 41a0 0000910 0000 41a0 0000 41a0 0000 41a0 0000 0000 0000920 0000 0000 0000 0000 0000 0000 0000 0000 0000930 0000 3f80 be7b 458a 0000 0000 4274 4437 0000940 622b 42e6 0000 4080 592a 4182 1c3f 4154 0000950 04be 43ac b2a0 3d9e 667d 44d0 a4be c338 0000960 670b 439f 8d86 4092 6426 3e33 59c4 c009 0000970 5832 c081 0529 bf77 92a8 bdd2 5c71 3e77 0000980 1d95 3e52 a795 3e8e 2f83 3f70 c978 41f8 0000990 9dd2 c21e e242 c1c6 a0d5 c24e 1d69 4286 00009a0 45ee c276 14bb c387 5332 3d70 c256 4194 00009b0 cbd6 4254 c4ec c06a 90a8 4210 0000 0000 00009c0 0000 0000 0000 0000 0000 0000 0000 4000 00009d0 20d1 3e1e 6b66 3f42 0000 0000 9251 441e 00009e0 0000 3f80 0000 40a0 0000 0000 0000 0000 00009f0 0000 0000 0000 0000 0000 0000 0000 0000 * 0000a10 0000 0000 0000 41a0 0000 41a0 0000 41a0 0000a20 0000 41a0 0000 0000 0000 0000 0000 0000 0000a30 0000 0000 0000 0000 0000 3f80 be7b 458a 0000a40 0000 0000 4274 4437 622b 42e6 0000 4080 0000a50 641f 4182 3229 4154 072e 43ac b4e0 3d9e 0000a60 6685 44d0 a7b1 c338 644a 439f 75b0 4091 0000a70 4e62 3e4b 36ec c00a aca6 c07f 24d9 bf75 0000a80 97c7 bdf3 5cb3 3e86 4df7 3e60 111a 3e95 0000a90 674e 3f6e d800 41fd 0f5d c220 cb6f c1d2 0000aa0 cd86 c24e 55b3 430c bfdb c25c 8ec7 c383 0000ab0 0962 4080 7334 4188 fe5d 4257 c4ec c06a 0000ac0 90a8 4210 0000 0000 0000 0000 0000 0000 0000ad0 0000 0000 0000 4000 d4fa 3e23 bc78 3f5b 0000ae0 0000 0000 2809 441d 0000 3f80 0000 40a0 0000af0 0000 0000 0000 0000 0000 0000 0000 0000 * 0000b10 0000 0000 0000 0000 0000 0000 0000 41a0 0000b20 0000 41a0 0000 41a0 0000 41a0 0000 0000 0000b30 0000 0000 0000 0000 0000 0000 0000 0000 0000b40 0000 3f80 be7b 458a 0000 0000 4274 4437 0000b50 622b 42e6 0000 4080 6eee 4182 47c6 4154 0000b60 0960 43ac b6e6 3d9e 668e 44d0 aa9e c338 0000b70 619b 439f 429c 4090 9c2c 3e64 cbf8 c00a 0000b80 89ab c07c 1841 bf73 3d4f be0a ddc7 3e90 0000b90 c0c9 3e6d 7072 3e9b 9080 3f6c c50c 4202 0000ba0 630d c221 37a8 c1de e6f5 c24e 19f3 4346 0000bb0 7bbe c250 56d4 c37f a2a0 40d1 dea8 4176 0000bc0 7e17 425b c4ec c06a 90a8 4210 0000 0000 0000bd0 0000 0000 0000 0000 0000 0000 0000 4000 0000be0 8924 3e25 a2de 3f6e 0000 0000 a3b8 441b 0000bf0 0000 3f80 0000 40a0 0000 0000 0000 0000 0000c00 0000 0000 0000 0000 0000 0000 0000 0000 * 0000c20 0000 0000 0000 41a0 0000 41a0 0000 41a0 0000c30 0000 41a0 0000 0000 0000 0000 0000 0000 0000c40 0000 0000 0000 0000 0000 3f80 be7b 458a 0000c50 0000 0000 4274 4437 622b 42e6 0000 4080 0000c60 79a4 4182 5d32 4154 0b56 43ac b8b5 3d9e 0000c70 6698 44d0 ad86 c338 5efb 439f e61d 408e 0000c80 02cd 3e80 0d7a c00b 2d0f c079 dd3b bf70 0000c90 b70f be1a 3be9 3e9b 84f7 3e7a caf9 3ea1 0000ca0 ab1e 3f6a 05af 4208 a074 c222 36ad c1e9 0000cb0 f207 c24e 155c 4388 2580 c242 19a1 c378 0000cc0 705d 4114 4558 415a 5cfd 425f c4ec c06a 0000cd0 90a8 4210 0000 0000 0000 0000 0000 0000 0000ce0 0000 0000 0000 4000 c003 3e2c 4b50 3f85 0000cf0 0000 0000 08ca 441a 0000 3f80 0000 40a0 0000d00 0000 0000 0000 0000 0000 0000 0000 0000 * 0000d20 0000 0000 0000 0000 0000 0000 0000 41a0 |
'모종의 음모 > motion simulator' 카테고리의 다른 글
| SFX-100 (0) | 2024.10.28 |
|---|---|
| f1 (게임) motion data packet (1) | 2024.10.27 |
| FFBchecker + Driving Force GT (2) | 2024.10.22 |
| codemaster telemetry (5) | 2024.10.22 |
| joyston air twister fx on linux (0) | 2024.10.21 |