[링크 : https://support.ircam.fr/docs/AudioSculpt/3.0/co/FFT%20Size.html]
[링크 : https://dsp.stackexchange.com/questions/47448/window-periodoverlap-and-fft]
[링크 : https://m.blog.naver.com/suya309/221467948212]
| fft 결과의 amplitude가 0.5가 나오는 이유 (0) | 2023.06.13 |
|---|---|
| overlap kissfft (0) | 2023.06.12 |
| fftw 라이브러리 사용 테스트 (0) | 2023.06.12 |
| fft 잘못 사용하고 있었나? (0) | 2023.06.02 |
| fft 라이브러리 목록 (0) | 2023.06.01 |
fftw()에
1. 입력 범위는 크게 의미 없으나 0.0~1.0 사이로 1의 높이로 정규화 하는 것이 용이할 수도 있음
2. DC 성분은 fft_result[0]에 있으며 / Sample 을 하면 DC 성분의 높이를 알 수 있음
2. sine() 성분은 fft_result[1~1/N]에 있으며 / Sample 을 하면 sine() 성분의 높이를 알 수 있음. (+/- x로 해석?)
3. phase는 모르겠다 -ㅁ-
-----------------
입력 값 범위 테스트
그냥 정상적인 0~1 사이의 실수 범위 입력
| for ( i = 0; i < n; i++ ) in[i] = ( double ) sin ( 360.0f * (double)i / n * 3.1415927f / 180.0f); |
입력 범위 확인
출력 결과
도대체.. 1Hz 에서 32는 무슨 의미냐..
샘플링 횟수로 나눌게 아니라 최대 주파수 로 나누어야 하는건가?
| Input Data: 0, 0.000000 1, 0.098017 2, 0.195090 ... Output FFT Coefficients: 0, -0.000000, 0.000000, 0.000000 1, 0.000003, -32.000000, 32.000000 2, -0.000000, 0.000001, 0.000001 |
걍 무지성으로 100,000 곱하기(0 다섯개)
| for ( i = 0; i < n; i++ ) in[i] = ( double ) sin ( 360.0f * (double)i / n * 3.1415927f / 180.0f) * 100000; |
FFT 결과 자체는 동일하지만(?) 결과 자체는 곱해준 100,000 만큼 증가
| Input Data: 0, 0.000000 1, 9801.714305 2,19509.032738 ... Output FFT Coefficients: 0, -0.008742, 0.000000, 0.008742 1, 0.271011,-3199999.955619,3200000.000000 2, -0.008742, 0.118444, 0.118767 |
위상(phase)
동일 값, 위치만 8 칸 미룸(8/64 = 1/8 phase)
phase는 atan(b/a) 로 계산한다는데 일단 하라는대로 하니, -1.5 대충 pi/2 정도 최대값으로 나오는 듯.
| Input Data: 0, 0.000000 1, 9801.714305 2,19509.032738 3,29028.468510 4,38268.344246 5,47139.674887 6,55557.024665 7,63439.329895 8,70710.679664 9,77301.046896 10,83146.962748 11,88192.127851 12,92387.954506 13,95694.034604 14,98078.528786 15,99518.473069 16,100000.000000 Output FFT Coefficients: 0, -0.008742, 0.000000, 0.008742, 3.141593 1, 0.271011,-3199999.955619,3199999.955619, -1.570796 2, -0.008742, 0.118444, 0.118767, 1.644472 |
Input Data: 0,70710.679664 1,77301.046896 2,83146.962748 3,88192.127851 4,92387.954506 5,95694.034604 6,98078.528786 7,99518.473069 8,100000.000000 9,99518.472212 10,98078.527081 11,95694.032066 12,92387.951160 13,88192.123730 14,83146.957891 15,77301.041350 16,70710.673482 Output FFT Coefficients: 0, 0.119650, 0.000000, 0.119650, 0.000000 1,2262741.972266,-2262741.421146,3199999.995629, -0.785398 2, -0.048261, 0.083753, 0.096663, 2.093553 |
[링크 : https://blog.naver.com/lyb0684/221159899932]
atan과 atan2는 범위가 다르다고 한다. (범위가 달라지는 거지 radian을 degree로 계산하는게 달라지는건 아니니..)
| atan RETURN VALUE On success, these functions return the principal value of the arc tan‐ gent of x in radians; the return value is in the range [-pi/2, pi/2]. atan2 RETURN VALUE On success, these functions return the principal value of the arc tan‐ gent of y/x in radians; the return value is in the range [-pi, pi]. |
아무튼 귀찮으니 atan2의 radian 값 출력을 각도로 변환해서 출력해보면
| for ( i = 0; i < nc; i++ ) { printf ( " %3d,%12f,%12f,%12f,%12f,%12f\n", i, out[i][0], out[i][1], sqrt(out[i][0] * out[i][0] + out[i][1] * out[i][1]), atan2(out[i][1], out[i][0]) * 180 / PI, atan(out[i][1] / out[i][0]) * 180 / PI } |
[링크 : https://spiralmoon.tistory.com/entry/프로그래밍-이론-두-점-사이의-절대각도를-재는-atan2]
뭔가 잘못 계산한 느낌이다?
| + 0 | 1, 0.000003, -32.000000, 32.000000, -89.999993, -89.999993 |
| + 8 | 1, 22.627420, -22.627414, 32.000000, -44.999992, -44.999992 |
| + 16 | 1, 32.000000, 0.000004, 32.000000, 0.000008, 0.000008 |
| + 32 | 1, -0.000006, 32.000000, 32.000000, 90.000007, -89.999988 |
+
DC성분
아래와 같이 1.0 값으로 64개를 만들어 fft를 돌리면
| for ( i = 0; i < n; i++ ) { in[i] = ( double )1.0f; } |
64번 샘플링한게 1씩 있어서 합산하여 64가 나오나?
아무튼 실수부의 경우 -와 +의 차이가 있지만 abs()로 처리하면 부호가 사라지니 같은 값으로 보이게 된다.
| Output FFT Coefficients: 0, 64.000000, 0.000000, 64.000000, 0.000000, 0.000000, 0.000000 |
| Output FFT Coefficients: 0, -64.000000, 0.000000, 64.000000, 3.141593, 179.999995, -0.000000 |
0.5로 하면 32가 나온다. 도대체 이 DC는 어떻게 해석해야 할까?
| Output FFT Coefficients: 0, 32.000000, 0.000000, 32.000000, 0.000000, 0.000000, 0.000000 |
sin() * 0.5는 DC 성분이 0으로 나오고 1Hz 에서는 16 으로 나온다(0.5로 봐야하나?)
| Output FFT Coefficients: 0, -0.000000, 0.000000, 0.000000, 3.141593, 179.999995, -0.000000 1, 0.000001, -16.000000, 16.000000, -1.570796, -89.999993, -89.999993 2, -0.000000, 0.000001, 0.000001, 1.644472, 94.221297, -85.778698 |
sin() * 0.5 + 0.5(0.0~1.0=1.0) 하면 DC 32에 1Hz 16 (1 * 16?)
걍 맘편하게 주파수는 진폭, DC는
| Output FFT Coefficients: 0, 32.000000, 0.000000, 32.000000, 0.000000, 0.000000, 0.000000 1, 0.000001, -16.000000, 16.000000, -1.570796, -89.999993, -89.999993 2, -0.000000, 0.000001, 0.000001, 1.644472, 94.221297, -85.778698 |
sin() 은(-1.0~1.0=2.0 Height?) DC 0 1Hz 32 (2 * 16?)
| Output FFT Coefficients: 0, -0.000000, 0.000000, 0.000000, 3.141593, 179.999995, -0.000000 1, 0.000003, -32.000000, 32.000000, -1.570796, -89.999993, -89.999993 |
sin() * 0.5 + 0.5 (0.0~1.0=1.0) 에 절반의 파형만 줄 경우
1Hz에 18
| Output FFT Coefficients: 0, 26.177734, 0.000000, 26.177734, 0.000000, 0.000000, 0.000000 1, 0.500000, -18.177734, 18.184609, -1.543297, -88.424406, -88.424406 2, -3.403504, -0.000000, 3.403504, -3.141593, -179.999990, 0.000005 |
sin(2x)
sin 주기가 늘어났다고 해서 16이 아니게 되는건 또 아니네?
그 와중에 0.5의 DC는 또 32.. 도대체 머냐고?!
0.5 * 64 = 32
sine 16/32 = 0.5. 혹시 +-0.5 라는건가?
| Output FFT Coefficients: 0, 32.000000, 0.000000, 32.000000, 0.000000, 0.000000, 0.000000 1, -0.000000, -0.000001, 0.000001, -1.716660, -98.357374, 81.642621 2, 0.000003, -16.000000, 16.000000, -1.570796, -89.999988, -89.999988 3, -0.000000, 0.000001, 0.000001, 1.652756, 94.695926, -85.304069 4, -0.000000, 0.000001, 0.000001, 1.718417, 98.458014, -81.541981 |
혹시나 해서 sin(2x) * 0.1 + 0.9 해보는데
57.6
산술적으로는 64 * 0.9 = 57.6
3.2 / 32 = 0.1 이니.. DC랑 혼합될 때랑 단독일때랑 다르게 나오나?
(+- 0.1 로 해석하면 쉬울지도?)
| Output FFT Coefficients: 0, 57.600000, 0.000000, 57.600000, 0.000000, 0.000000, 0.000000 1, -0.000000, -0.000000, 0.000000, -1.716660, -98.357374, 81.642621 2, 0.000001, -3.200000, 3.200000, -1.570796, -89.999988, -89.999988 3, -0.000000, 0.000000, 0.000000, 1.652756, 94.695926, -85.304069 |
sin(2x)의 절반 파형만 도배!
고조파 처럼 나오네?
DC 52.3
4Hz 6.8, 8Hz 1.42, 12Hz 0.65, 16Hz 0.39, 20Hz 0.28, 24Hz 0.23, 28Hz0.20, 32Hz 0.19 (합계 10.251662)
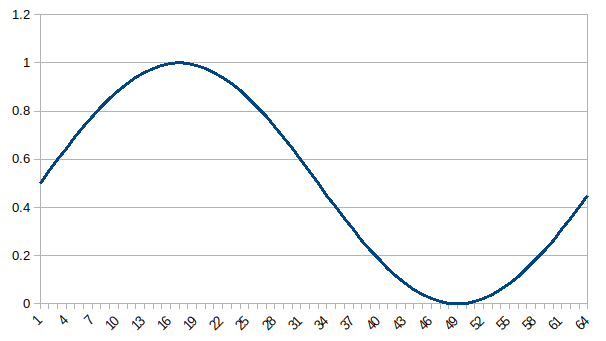
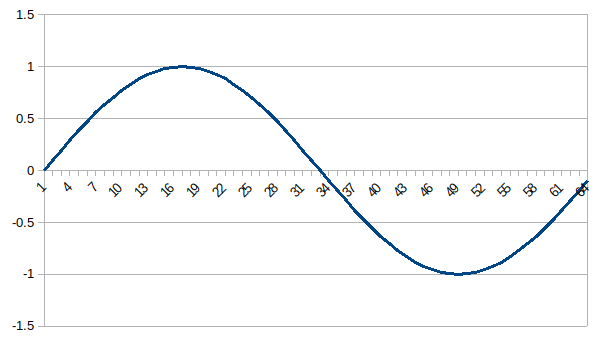
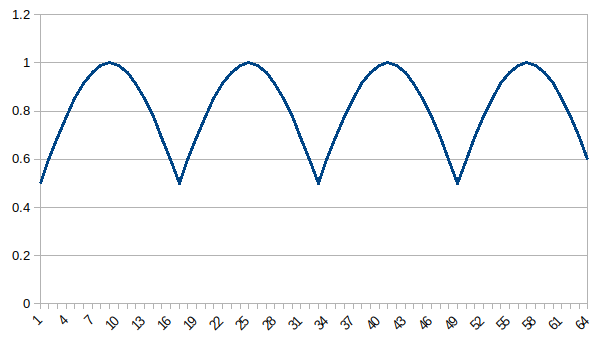
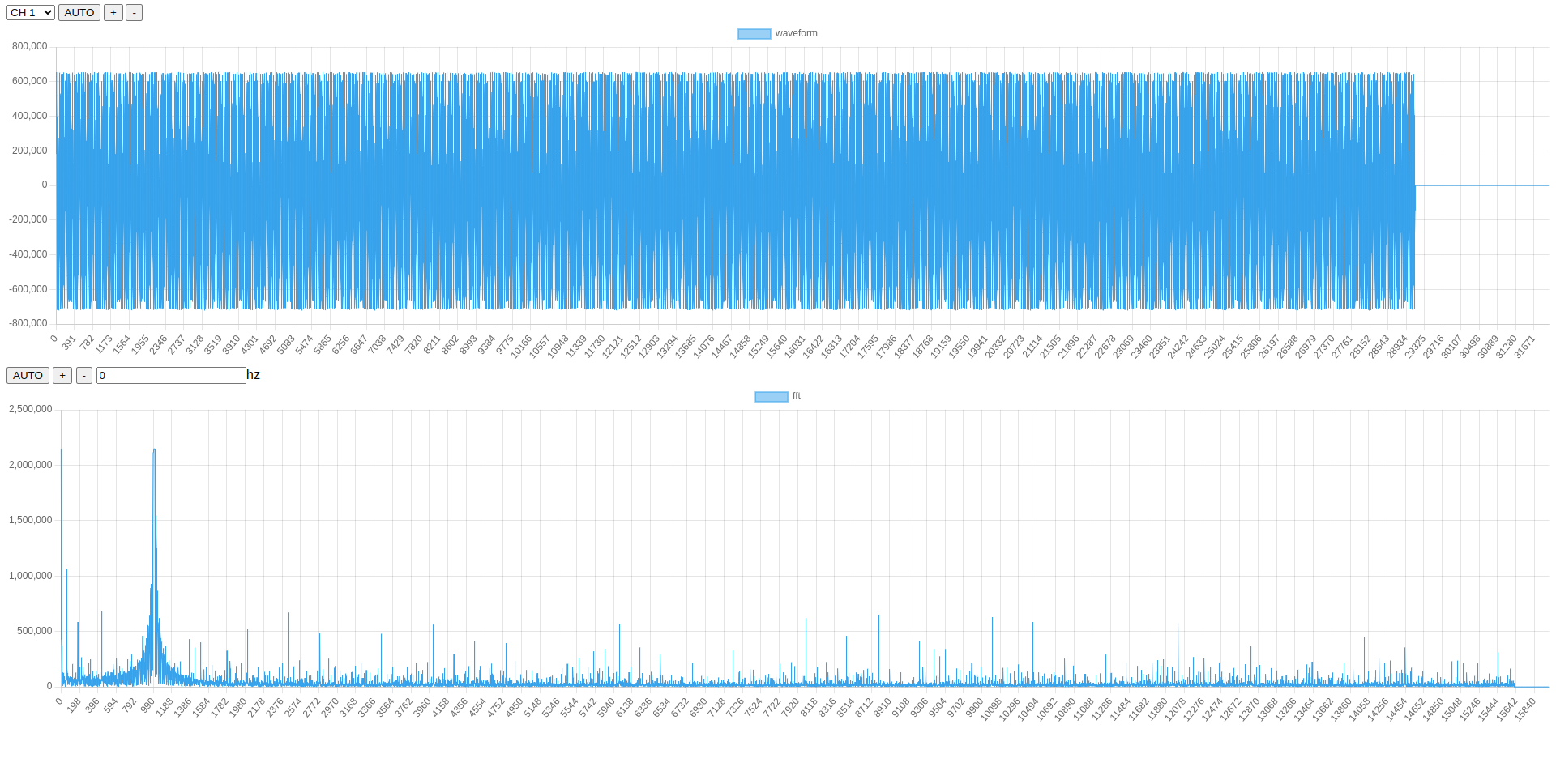
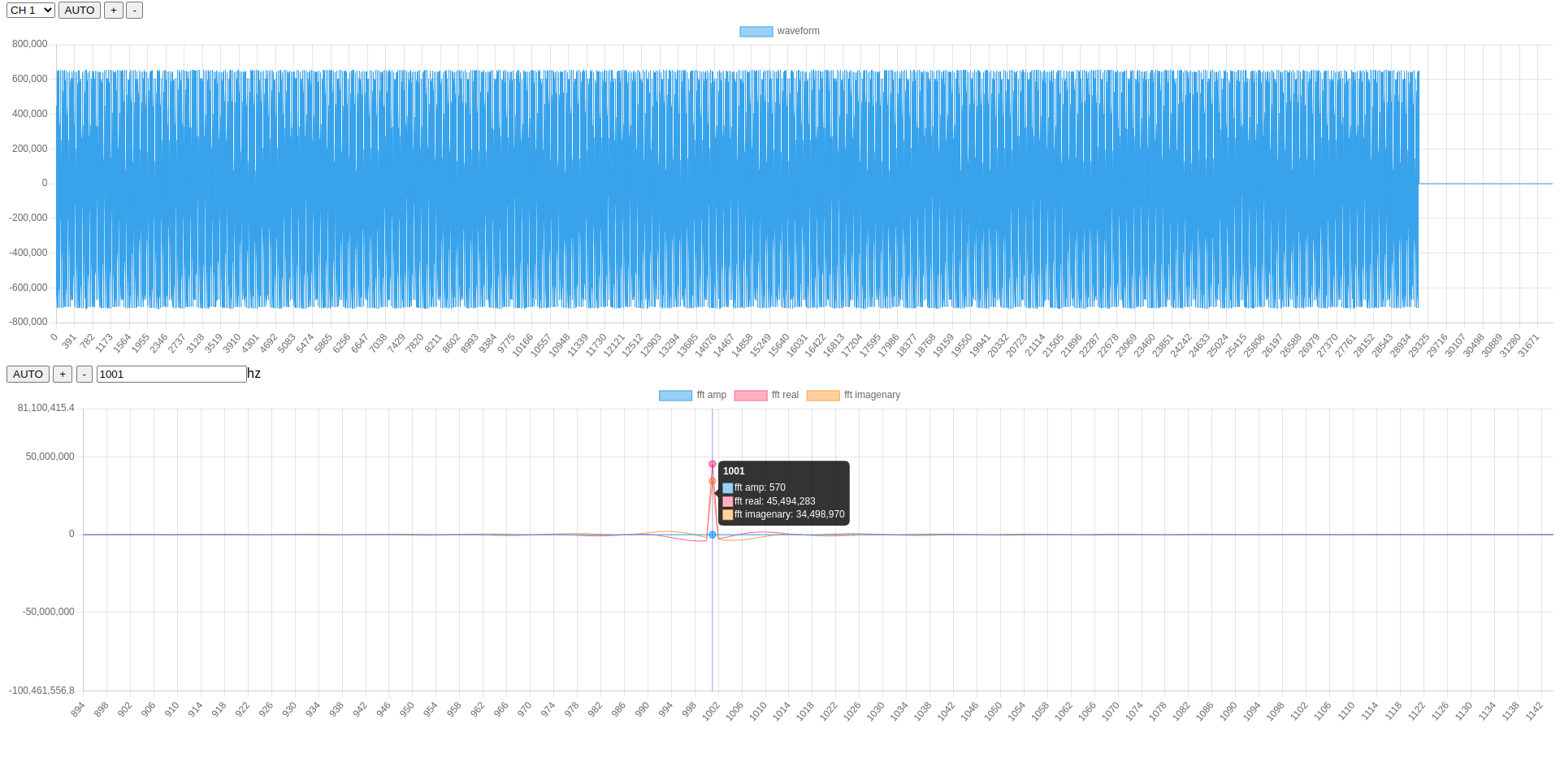
| Output FFT Coefficients: 0, 52.306340, 0.000000, 52.306340, 0.000000, 0.000000, 0.000000 1, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 2, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 3, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 4, -6.856612, -0.000001, 6.856612, -3.141593, -179.999990, 0.000005 5, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 6, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 7, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 8, -1.425690, -0.000000, 1.425690, -3.141592, -179.999986, 0.000009 9, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 10, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 11, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 12, -0.652365, -0.000000, 0.652365, -3.141592, -179.999983, 0.000012 13, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 14, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 15, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 16, -0.397825, -0.000000, 0.397825, -3.141592, -179.999982, 0.000013 17, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 18, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 19, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 20, -0.286168, -0.000000, 0.286168, -3.141592, -179.999983, 0.000012 21, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 22, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 23, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 24, -0.231164, -0.000000, 0.231164, -3.141592, -179.999986, 0.000009 25, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 26, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 27, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 28, -0.204855, -0.000000, 0.204855, -3.141593, -179.999990, 0.000005 29, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 30, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 31, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 32, -0.196983, 0.000000, 0.196983, 3.141593, 179.999995, -0.000000 |
| overlap kissfft (0) | 2023.06.12 |
|---|---|
| fft size overlap window size (0) | 2023.06.12 |
| fft 잘못 사용하고 있었나? (0) | 2023.06.02 |
| fft 라이브러리 목록 (0) | 2023.06.01 |
| fftw 다차원 분석 (0) | 2023.05.27 |
입력값을 정규화 하려고 했는데
fftw를 쓴다고 알려진 matlab의 예제를 보니
입력값 범위로 정규화하는게 아니라(입력 값이 8bit 라면 /256 으로 0~1 사이 값으로..)
입력 받는 샘플의 갯수로 정규화 해줘야 하는 건가?
아무튼 정규화 했다고 생각했는데 진폭이 이상하게 1이상의 값이 나왔는데
그거 탓이었나 싶기도 하고.. 다시 테스트 해봐야 할 듯
| Fs = 1000; % Sampling frequency T = 1/Fs; % Sampling period L = 1500; % Length of signal t = (0:L-1)*T; % Time vector 푸리에 변환을 계산합니다. Y = fft(X); 양방향 스펙트럼 P2를 계산합니다. 그런 다음, P2와 짝수 값 신호 길이 L을 기반으로 하여 단방향 스펙트럼 P1을 계산합니다. P2 = abs(Y/L); P1 = P2(1:L/2+1); P1(2:end-1) = 2*P1(2:end-1); |
[링크 : https://kr.mathworks.com/help/matlab/ref/fft.html]
| fftw_plan fftw_plan_r2r_1d(int n, double *in, double *out, fftw_r2r_kind kind, unsigned flags); fftw_plan fftw_plan_r2r_2d(int n0, int n1, double *in, double *out, fftw_r2r_kind kind0, fftw_r2r_kind kind1, unsigned flags); fftw_plan fftw_plan_r2r_3d(int n0, int n1, int n2, double *in, double *out, fftw_r2r_kind kind0, fftw_r2r_kind kind1, fftw_r2r_kind kind2, unsigned flags); fftw_plan fftw_plan_r2r(int rank, const int *n, double *in, double *out, const fftw_r2r_kind *kind, unsigned flags); |
[링크 : https://www.fftw.org/fftw3_doc/More-DFTs-of-Real-Data.html]
| fft size overlap window size (0) | 2023.06.12 |
|---|---|
| fftw 라이브러리 사용 테스트 (0) | 2023.06.12 |
| fft 라이브러리 목록 (0) | 2023.06.01 |
| fftw 다차원 분석 (0) | 2023.05.27 |
| fft phase 연산 (0) | 2023.04.07 |
[링크 : https://community.vcvrack.com/t/complete-list-of-c-c-fft-libraries/9153]
BSD like. arm
[링크 : https://bitbucket.org/jpommier/pffft/src/master/]
bsd 3 clause. x86 (Makefile)
[링크 : https://github.com/mborgerding/kissfft]
bsd 3 clause. arm 언급 없음
[링크 : https://gitlab.mpcdf.mpg.de/mtr/pocketfft/tree/cpp]
public
[링크 : https://netlib.org/fftpack/]
apache
| fftw 라이브러리 사용 테스트 (0) | 2023.06.12 |
|---|---|
| fft 잘못 사용하고 있었나? (0) | 2023.06.02 |
| fftw 다차원 분석 (0) | 2023.05.27 |
| fft phase 연산 (0) | 2023.04.07 |
| fftw input range? (0) | 2023.04.07 |
libttfw 에서는 2차원 3차원 DFT를 지원하는데, 내가 생각하는 그 2차원 3차원이 맞나 모르겠다.
센서가 3축이면 3차원은 맞긴한데.. 희소행렬 형태로 삽입이 되어야 하나?
| 2.2 Complex Multi-Dimensional DFTs Multi-dimensional transforms work much the same way as one-dimensional transforms: you allocate arrays of fftw_complex (preferably using fftw_malloc), create an fftw_plan, execute it as many times as you want with fftw_execute(plan), and clean up with fftw_destroy_plan(plan) (and fftw_free). FFTW provides two routines for creating plans for 2d and 3d transforms, and one routine for creating plans of arbitrary dimensionality. The 2d and 3d routines have the following signature: fftw_plan fftw_plan_dft_2d(int n0, int n1, fftw_complex *in, fftw_complex *out, int sign, unsigned flags); fftw_plan fftw_plan_dft_3d(int n0, int n1, int n2, fftw_complex *in, fftw_complex *out, int sign, unsigned flags); |
[링크 : https://www.fftw.org/fftw3_doc/Complex-Multi_002dDimensional-DFTs.html]
| 3.2.1 Row-major Format The multi-dimensional arrays passed to fftw_plan_dft etcetera are expected to be stored as a single contiguous block in row-major order (sometimes called “C order”). Basically, this means that as you step through adjacent memory locations, the first dimension’s index varies most slowly and the last dimension’s index varies most quickly. To be more explicit, let us consider an array of rank d whose dimensions are n0 × n1 × n2 × … × nd-1 . Now, we specify a location in the array by a sequence of d (zero-based) indices, one for each dimension: (i0, i1, i2,..., id-1). If the array is stored in row-major order, then this element is located at the position id-1 + nd-1 * (id-2 + nd-2 * (... + n1 * i0)). Note that, for the ordinary complex DFT, each element of the array must be of type fftw_complex; i.e. a (real, imaginary) pair of (double-precision) numbers. In the advanced FFTW interface, the physical dimensions n from which the indices are computed can be different from (larger than) the logical dimensions of the transform to be computed, in order to transform a subset of a larger array. Note also that, in the advanced interface, the expression above is multiplied by a stride to get the actual array index—this is useful in situations where each element of the multi-dimensional array is actually a data structure (or another array), and you just want to transform a single field. In the basic interface, however, the stride is 1. |
[링크 : https://www.fftw.org/fftw3_doc/Row_002dmajor-Format.html]
| A multi-dimensional array whose size is declared at compile time in C is already in row-major order. You don’t have to do anything special to transform it. For example: { fftw_complex data[N0][N1][N2]; fftw_plan plan; ... plan = fftw_plan_dft_3d(N0, N1, N2, &data[0][0][0], &data[0][0][0], FFTW_FORWARD, FFTW_ESTIMATE); ... } This will plan a 3d in-place transform of size N0 x N1 x N2. Notice how we took the address of the zero-th element to pass to the planner (we could also have used a typecast). |
[링크 : https://www.fftw.org/fftw3_doc/Fixed_002dsize-Arrays-in-C.html]
[링크 : https://www.fftw.org/fftw3_doc/Multi_002ddimensional-Array-Format.html]
+
에라이 모르겠다 ㅠㅠ
| switch (sz->rnk) { case 1: if (p->sign < 0) { if (verbose > 2) printf("using plan_dft_r2c_1d\n"); return FFTW(plan_dft_r2c_1d)(sz->dims[0].n, (bench_real *) p->in, (bench_complex *) p->out, flags); } else { if (verbose > 2) printf("using plan_dft_c2r_1d\n"); return FFTW(plan_dft_c2r_1d)(sz->dims[0].n, (bench_complex *) p->in, (bench_real *) p->out, flags); } break; case 2: if (p->sign < 0) { if (verbose > 2) printf("using plan_dft_r2c_2d\n"); return FFTW(plan_dft_r2c_2d)(sz->dims[0].n, sz->dims[1].n, (bench_real *) p->in, (bench_complex *) p->out, flags); } else { if (verbose > 2) printf("using plan_dft_c2r_2d\n"); return FFTW(plan_dft_c2r_2d)(sz->dims[0].n, sz->dims[1].n, (bench_complex *) p->in, (bench_real *) p->out, flags); } break; case 3: if (p->sign < 0) { if (verbose > 2) printf("using plan_dft_r2c_3d\n"); return FFTW(plan_dft_r2c_3d)( sz->dims[0].n, sz->dims[1].n, sz->dims[2].n, (bench_real *) p->in, (bench_complex *) p->out, flags); } else { if (verbose > 2) printf("using plan_dft_c2r_3d\n"); return FFTW(plan_dft_c2r_3d)( sz->dims[0].n, sz->dims[1].n, sz->dims[2].n, (bench_complex *) p->in, (bench_real *) p->out, flags); } break; default: { int *n = mkn(sz); if (p->sign < 0) { if (verbose > 2) printf("using plan_dft_r2c\n"); pln = FFTW(plan_dft_r2c)(sz->rnk, n, (bench_real *) p->in, (bench_complex *) p->out, flags); } else { if (verbose > 2) printf("using plan_dft_c2r\n"); pln = FFTW(plan_dft_c2r)(sz->rnk, n, (bench_complex *) p->in, (bench_real *) p->out, flags); } bench_free(n); return pln; } } |
[링크 : https://github.com/FFTW/fftw3/blob/master/tests/bench.c]
+
mpi 예제도 있음.
그런데 3d로 한다고 하니 어마어마하게 데이터가 필요할 것 같은데
단순하게 3축 데이터라면 엄청 큰 공간에 딱 3줄 넣는 식이 될텐데 어떻게 해야 할까?
| data = (FFTW_COMPLEX *) FFTW_MALLOC(sizeof(FFTW_COMPLEX) * NX*NY*NZ*sizeof(FFTW_COMPLEX)); /* create plan for forward DFT */ gettimeofday(&tv_start, NULL); plan = FFTW_PLAN_DFT_3D(NX, NY, NZ, data, data, FFTW_FORWARD, FFTW_ESTIMATE); gettimeofday(&tv_stop, NULL); deltaT = tv_stop.tv_sec - tv_start.tv_sec + 1e-6 * (tv_stop.tv_usec - tv_start.tv_usec); printf("Plan init time (c2c) : %f sec\n", deltaT); /* initialize data */ for (i = 0; i < NX; ++i) { for (j = 0; j < NY; ++j) { for (k = 0; k < NZ; ++k) { data[(i*NY + j)*NZ + k][0] = (i*NY + j)*NZ + k; data[(i*NY + j)*NZ + k][1] = 0; } } } |
[링크 : https://github.com/pkestene/simpleFFTW/blob/master/c/fftw_test_3d_serial.c]
+
암만봐도 2d나 3d fft는 어떻게 써야 할지 감도 안와서 사용 시도 자체를 포기!
| fft 잘못 사용하고 있었나? (0) | 2023.06.02 |
|---|---|
| fft 라이브러리 목록 (0) | 2023.06.01 |
| fft phase 연산 (0) | 2023.04.07 |
| fftw input range? (0) | 2023.04.07 |
| fft 복소수(complex) - 실수, 허수부(real, imaginary) (0) | 2023.04.07 |
x 축은 real(실수)
y 축은 imagenary(허수)
그래서 arctan(허수/실수) 하면 각도를 radian으로 구할수 있다.
javascript 기준으로는
Math.atan() * 180 / Math.PI 하면 각도로 전환가능
| θ = tan- 1 (b/a) |
[링크 : http://sites.music.columbia.edu/cmc/MusicAndComputers/popups/chapter3/xbit_3_3.php]
역시나 언제나 그렇듯 radian 값
[링크 : https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Math/atan]
| fft 라이브러리 목록 (0) | 2023.06.01 |
|---|---|
| fftw 다차원 분석 (0) | 2023.05.27 |
| fftw input range? (0) | 2023.04.07 |
| fft 복소수(complex) - 실수, 허수부(real, imaginary) (0) | 2023.04.07 |
| fft 0 Hz (2) | 2023.04.05 |
chatGPT는 아래와 같이 대답을 하는데 근거가 없어서 불안하고
| The input float range for FFTW depends on the specific implementation and the configuration of the library. However, in general, the input float values should be within the range of -1.0 to 1.0, which represents the normalized range of the input signal. |
stackoverflow는 과거 글이긴 한데.. 미묘..
| Surprisingly there is no single agreed definition for the FFT and the IFFT, at least as far as scaling is concerned, but for most implementations (including FFTW) you need to scale by 1/N in the forward direction, and there is no scaling in the reverse direction. Usually (for performance reasons) you will want to lump this scaling factor in with any other corrections, such as your A/D gain, window gain correction factor, etc, so that you just have one combined scale factor to apply to your FFT output bins. Alternatively if you are just generating, say, a power spectrum in dB then you can make the correction a single dB value that you subtract from your power spectrum bins. |
[링크 : https://stackoverflow.com/questions/4855958/normalising-fft-data-fftw]
일단은 실험!
1. 원본 데이터 그대로
+-1V / 1.001Khz
-600,000 ~ +600,000 범위로 들어오는 값을 그대~~~로 FFT로 던지니 결과가 이상하게 나온다.
2. 원본 / 1000
범위를 벗어나진 않아서 그런가 정상적으로 그나마 주파수 분석이 되는 듯
3. 원본 / 100
/ 1000 이랑 비슷하긴 한데 비율 때문에 그런가 중심 주파수 주변에 좀 높게 나온다.
그냥 나누기 만큼의 억제효과가 나오는 듯?
4. 원본 / 838607 (0x7FFFFF 왜 이런 값을 했지.. 홀렸나..)
주파수 분석결과를 확대해보면 /1000 보단 깨끗하게 분석된다.
5. 원본 + 100mV
FFT 값에 2,147,483이 나와서 16진수로 바꾸어 보니 0x20C49B
무슨 의미를 지닌 분석이라고 보기 힘든데 그래도 1000 근처에 좀 비어있는거 보면 어떻게 해석해야 하나 싶다.
6. 원본 / 24bit(0xFFFFFF)
아 몰랑 걍 -1.0 ~ 1.0 사이로 정규화 할래!
| fftw 다차원 분석 (0) | 2023.05.27 |
|---|---|
| fft phase 연산 (0) | 2023.04.07 |
| fft 복소수(complex) - 실수, 허수부(real, imaginary) (0) | 2023.04.07 |
| fft 0 Hz (2) | 2023.04.05 |
| partial fft (0) | 2023.04.04 |
내 프로그램에서도 한번 도식화 해볼까?
amplitude만 보는데 real 값과 imaginary 값은 어떻게 보여질지 궁금해서 찾아보는데
그렇게는 잘 안써서 그런지 그림도 찾기 힘들다.
[링크 : https://stackoverflow.com/questions/25624548/fft-real-imaginary-abs-parts-interpretation]
+
부랴부랴 수정해서 확인해보니 실수부, 허수부는 * 100,000 해서 받아와서 표현
일단 네 가지 데이터가 오가면서 출력되는데 이걸 phase 라고 보야하려나?
실수, 허수 둘 다 양수
실수, 허수 둘 다 음수
실수 양수, 허수 음수
실수 음수, 허수 양수
| fft phase 연산 (0) | 2023.04.07 |
|---|---|
| fftw input range? (0) | 2023.04.07 |
| fft 0 Hz (2) | 2023.04.05 |
| partial fft (0) | 2023.04.04 |
| fftw plan (0) | 2023.03.31 |
정리하자면
FFT를 100개 하면, 1~50 Hz와 0Hz에 대한 분석 결과가 나온다.
그래서 N / 2 + 1개
---
도대체 왜 N/2+1이 나오나를 찾는데 이해를 못하겠다.
| For a real-to-complex transform you get N / 2 + 1 complex outputs for N real inputs (the redundant symmetric outputs are not generated). The 0 Hz component is in bin 0. |
| Now out contains r0, r1, r2, ..., rn/2, i(n+1)/2-1, ..., i2, i1 , as it is written in the manual. r0 ,out[0],is the mean value of your data/signal. r1 ,out[1],is the real part of the first element of the DFT. ... i0 is 0 because you're using real data , so it isn't stored in out. i1 ,out[N-1],is the imaginary part of the first element of the DFT. i2 ,out[N-2],is the imaginary part of the second element of the DFT. If N is a even number , then r(N/2) out[N/2] is the Nyquist frequency amplitude. Im new to fftw library Remember that FFTW computes only the product of your data by the trigonometric functions, but it don't normalize them. You can find more info about the halfcomplex here. |
[링크 : https://kr.mathworks.com/matlabcentral/answers/42325-fft-is-finding-a-max-amplitude-at-0-hz]
chatGPT
| The reason that the Fast Fourier Transform (FFT) in the library FFTW produces a result of N/2+1 values when applied to real input data of length N is because of the way that the FFT algorithm works. In FFTW, the FFT algorithm used is called the "real-to-complex" FFT, which takes real-valued input data and produces complex-valued output data. When applied to real input data, the algorithm takes advantage of the symmetry properties of the Fourier transform of real-valued signals. Specifically, the Fourier transform of a real-valued signal is complex-conjugate symmetric, meaning that if x(t) is a real-valued signal, then its Fourier transform X(f) satisfies X(-f) = conj(X(f)), where "conj" denotes complex conjugation. Because of this symmetry property, half of the output values of the FFT algorithm are redundant, and can be calculated from the other half. Specifically, the output values for frequencies from 0 to N/2 are unique, while the output values for frequencies from N/2+1 to N-1 can be calculated as the complex conjugate of the corresponding frequency from 1 to N/2-1. Therefore, to save computation time and memory, FFTW only calculates the unique output values for frequencies from 0 to N/2, as well as the value for frequency N/2 (if N is even). This results in a total of N/2+1 output values. |
FFTW 라이브러리에서 Fast Fourier Transform (FFT)를 적용하면, 길이가 N인 실수 입력 데이터에 대해 복소수 출력 데이터 N/2+1개가 생성됩니다. 이는 FFT 알고리즘이 동작하는 방식 때문입니다. FFTW에서 사용되는 FFT 알고리즘은 "real-to-complex" FFT라고 불리며, 실수값 입력 데이터를 복소수값 출력 데이터로 변환합니다. 이 알고리즘은 실수값 신호의 푸리에 변환의 대칭성(symmetric) 특성을 활용합니다. 구체적으로, 실수값 신호 x(t)의 푸리에 변환 X(f)은 X(-f) = conj(X(f)) 라는 복소수 공액대칭성(complex-conjugate symmetric)을 만족합니다. 여기서 "conj"는 복소수 공액(conjugate)를 의미합니다. 이 대칭성 특성 때문에 FFT 알고리즘의 출력값 중 절반은 중복되는 값이며, 나머지 절반은 이 중복된 값들로부터 계산될 수 있습니다. 구체적으로, 0부터 N/2까지의 주파수 대역에서는 고유한 출력값이 존재하며, N/2+1부터 N-1까지의 주파수 대역에서는 대응하는 1부터 N/2-1까지의 주파수 대역의 복소수 공액값을 계산하여 구할 수 있습니다. 따라서 FFTW는 연산 시간과 메모리를 절약하기 위해, 0부터 N/2까지의 주파수 대역에 대한 고유한 출력값과, N이 짝수인 경우 주파수 N/2에 대한 출력값을 계산합니다. 이렇게 계산된 출력값의 총 개수는 N/2+1개가 됩니다. |
The DFT results are stored in-order in the array out, with the zero-frequency (DC) component in out[0].
+
2023.06.16
| Size of FFT in 1D is not half of the signal length. It's still the signal length (assuming FFT length was of the signal length). However for real data, due to conjugate symmetry, half of this is redundant and can be dicarded to reduce storage. Note however that, when it's required to process the FFT data, you have to construct the full length from the half and proceed. This is also the reason why spectral analysis software display only positive frequencies for real data; i.e, negative frequencies will be a mirror copy (of the magnitude) of positive frequencies. But you don't have to discard the half. You can just retain it. For image processing, the symmetry of FFT for real input data again exist and if you wish you can also dicard half of the image FFT data. Whether this will be employed or not depends on the intentions of the package. |
[링크 : https://brianmcfee.net/dstbook-site/content/ch06-dft-properties/Conjugate-Symmetry.html]
| fftw input range? (0) | 2023.04.07 |
|---|---|
| fft 복소수(complex) - 실수, 허수부(real, imaginary) (0) | 2023.04.07 |
| partial fft (0) | 2023.04.04 |
| fftw plan (0) | 2023.03.31 |
| libfftw3 precision (0) | 2023.03.30 |
이걸 어떻게 써먹어야 하나..
[링크 : http://www.fftw.org/pruned.html]
[링크 : https://www.fftw.org/faq/section3.html#pruned]
[링크 : https://velog.io/@cleansky/메모리-효율적으로-Partial-FFT-계수값-구하는-방법]
| fft 복소수(complex) - 실수, 허수부(real, imaginary) (0) | 2023.04.07 |
|---|---|
| fft 0 Hz (2) | 2023.04.05 |
| fftw plan (0) | 2023.03.31 |
| libfftw3 precision (0) | 2023.03.30 |
| spectrogram (0) | 2023.03.29 |
|
