fftw()에
1. 입력 범위는 크게 의미 없으나 0.0~1.0 사이로 1의 높이로 정규화 하는 것이 용이할 수도 있음
2. DC 성분은 fft_result[0]에 있으며 / Sample 을 하면 DC 성분의 높이를 알 수 있음
2. sine() 성분은 fft_result[1~1/N]에 있으며 / Sample 을 하면 sine() 성분의 높이를 알 수 있음. (+/- x로 해석?)
3. phase는 모르겠다 -ㅁ-
-----------------
입력 값 범위 테스트
그냥 정상적인 0~1 사이의 실수 범위 입력
| for ( i = 0; i < n; i++ ) in[i] = ( double ) sin ( 360.0f * (double)i / n * 3.1415927f / 180.0f); |
입력 범위 확인

출력 결과
도대체.. 1Hz 에서 32는 무슨 의미냐..
샘플링 횟수로 나눌게 아니라 최대 주파수 로 나누어야 하는건가?
| Input Data: 0, 0.000000 1, 0.098017 2, 0.195090 ... Output FFT Coefficients: 0, -0.000000, 0.000000, 0.000000 1, 0.000003, -32.000000, 32.000000 2, -0.000000, 0.000001, 0.000001 |
걍 무지성으로 100,000 곱하기(0 다섯개)
| for ( i = 0; i < n; i++ ) in[i] = ( double ) sin ( 360.0f * (double)i / n * 3.1415927f / 180.0f) * 100000; |
FFT 결과 자체는 동일하지만(?) 결과 자체는 곱해준 100,000 만큼 증가
| Input Data: 0, 0.000000 1, 9801.714305 2,19509.032738 ... Output FFT Coefficients: 0, -0.008742, 0.000000, 0.008742 1, 0.271011,-3199999.955619,3200000.000000 2, -0.008742, 0.118444, 0.118767 |
위상(phase)
동일 값, 위치만 8 칸 미룸(8/64 = 1/8 phase)
phase는 atan(b/a) 로 계산한다는데 일단 하라는대로 하니, -1.5 대충 pi/2 정도 최대값으로 나오는 듯.
| Input Data: 0, 0.000000 1, 9801.714305 2,19509.032738 3,29028.468510 4,38268.344246 5,47139.674887 6,55557.024665 7,63439.329895 8,70710.679664 9,77301.046896 10,83146.962748 11,88192.127851 12,92387.954506 13,95694.034604 14,98078.528786 15,99518.473069 16,100000.000000 Output FFT Coefficients: 0, -0.008742, 0.000000, 0.008742, 3.141593 1, 0.271011,-3199999.955619,3199999.955619, -1.570796 2, -0.008742, 0.118444, 0.118767, 1.644472 |
Input Data: 0,70710.679664 1,77301.046896 2,83146.962748 3,88192.127851 4,92387.954506 5,95694.034604 6,98078.528786 7,99518.473069 8,100000.000000 9,99518.472212 10,98078.527081 11,95694.032066 12,92387.951160 13,88192.123730 14,83146.957891 15,77301.041350 16,70710.673482 Output FFT Coefficients: 0, 0.119650, 0.000000, 0.119650, 0.000000 1,2262741.972266,-2262741.421146,3199999.995629, -0.785398 2, -0.048261, 0.083753, 0.096663, 2.093553 |
[링크 : https://blog.naver.com/lyb0684/221159899932]
atan과 atan2는 범위가 다르다고 한다. (범위가 달라지는 거지 radian을 degree로 계산하는게 달라지는건 아니니..)
| atan RETURN VALUE On success, these functions return the principal value of the arc tan‐ gent of x in radians; the return value is in the range [-pi/2, pi/2]. atan2 RETURN VALUE On success, these functions return the principal value of the arc tan‐ gent of y/x in radians; the return value is in the range [-pi, pi]. |
아무튼 귀찮으니 atan2의 radian 값 출력을 각도로 변환해서 출력해보면
| for ( i = 0; i < nc; i++ ) { printf ( " %3d,%12f,%12f,%12f,%12f,%12f\n", i, out[i][0], out[i][1], sqrt(out[i][0] * out[i][0] + out[i][1] * out[i][1]), atan2(out[i][1], out[i][0]) * 180 / PI, atan(out[i][1] / out[i][0]) * 180 / PI } |
[링크 : https://spiralmoon.tistory.com/entry/프로그래밍-이론-두-점-사이의-절대각도를-재는-atan2]
뭔가 잘못 계산한 느낌이다?
| + 0 | 1, 0.000003, -32.000000, 32.000000, -89.999993, -89.999993 |
| + 8 | 1, 22.627420, -22.627414, 32.000000, -44.999992, -44.999992 |
| + 16 | 1, 32.000000, 0.000004, 32.000000, 0.000008, 0.000008 |
| + 32 | 1, -0.000006, 32.000000, 32.000000, 90.000007, -89.999988 |
+
DC성분
아래와 같이 1.0 값으로 64개를 만들어 fft를 돌리면
| for ( i = 0; i < n; i++ ) { in[i] = ( double )1.0f; } |
64번 샘플링한게 1씩 있어서 합산하여 64가 나오나?
아무튼 실수부의 경우 -와 +의 차이가 있지만 abs()로 처리하면 부호가 사라지니 같은 값으로 보이게 된다.
| Output FFT Coefficients: 0, 64.000000, 0.000000, 64.000000, 0.000000, 0.000000, 0.000000 |
| Output FFT Coefficients: 0, -64.000000, 0.000000, 64.000000, 3.141593, 179.999995, -0.000000 |
0.5로 하면 32가 나온다. 도대체 이 DC는 어떻게 해석해야 할까?
| Output FFT Coefficients: 0, 32.000000, 0.000000, 32.000000, 0.000000, 0.000000, 0.000000 |
sin() * 0.5는 DC 성분이 0으로 나오고 1Hz 에서는 16 으로 나온다(0.5로 봐야하나?)
| Output FFT Coefficients: 0, -0.000000, 0.000000, 0.000000, 3.141593, 179.999995, -0.000000 1, 0.000001, -16.000000, 16.000000, -1.570796, -89.999993, -89.999993 2, -0.000000, 0.000001, 0.000001, 1.644472, 94.221297, -85.778698 |
sin() * 0.5 + 0.5(0.0~1.0=1.0) 하면 DC 32에 1Hz 16 (1 * 16?)
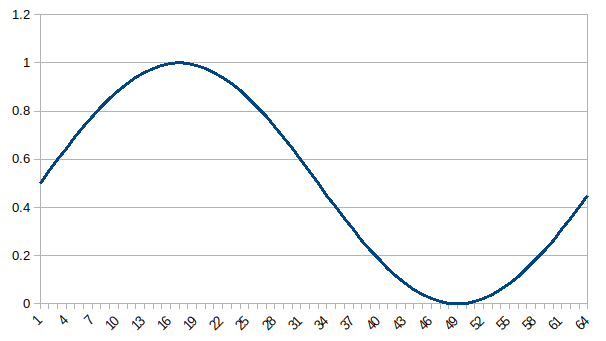
걍 맘편하게 주파수는 진폭, DC는
| Output FFT Coefficients: 0, 32.000000, 0.000000, 32.000000, 0.000000, 0.000000, 0.000000 1, 0.000001, -16.000000, 16.000000, -1.570796, -89.999993, -89.999993 2, -0.000000, 0.000001, 0.000001, 1.644472, 94.221297, -85.778698 |
sin() 은(-1.0~1.0=2.0 Height?) DC 0 1Hz 32 (2 * 16?)
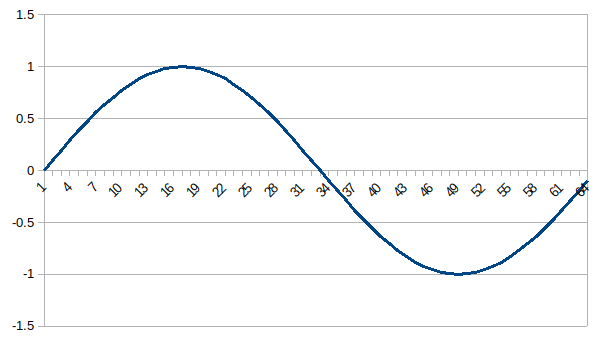
| Output FFT Coefficients: 0, -0.000000, 0.000000, 0.000000, 3.141593, 179.999995, -0.000000 1, 0.000003, -32.000000, 32.000000, -1.570796, -89.999993, -89.999993 |
sin() * 0.5 + 0.5 (0.0~1.0=1.0) 에 절반의 파형만 줄 경우
1Hz에 18

| Output FFT Coefficients: 0, 26.177734, 0.000000, 26.177734, 0.000000, 0.000000, 0.000000 1, 0.500000, -18.177734, 18.184609, -1.543297, -88.424406, -88.424406 2, -3.403504, -0.000000, 3.403504, -3.141593, -179.999990, 0.000005 |
sin(2x)

sin 주기가 늘어났다고 해서 16이 아니게 되는건 또 아니네?
그 와중에 0.5의 DC는 또 32.. 도대체 머냐고?!
0.5 * 64 = 32
sine 16/32 = 0.5. 혹시 +-0.5 라는건가?
| Output FFT Coefficients: 0, 32.000000, 0.000000, 32.000000, 0.000000, 0.000000, 0.000000 1, -0.000000, -0.000001, 0.000001, -1.716660, -98.357374, 81.642621 2, 0.000003, -16.000000, 16.000000, -1.570796, -89.999988, -89.999988 3, -0.000000, 0.000001, 0.000001, 1.652756, 94.695926, -85.304069 4, -0.000000, 0.000001, 0.000001, 1.718417, 98.458014, -81.541981 |
혹시나 해서 sin(2x) * 0.1 + 0.9 해보는데

57.6
산술적으로는 64 * 0.9 = 57.6
3.2 / 32 = 0.1 이니.. DC랑 혼합될 때랑 단독일때랑 다르게 나오나?
(+- 0.1 로 해석하면 쉬울지도?)
| Output FFT Coefficients: 0, 57.600000, 0.000000, 57.600000, 0.000000, 0.000000, 0.000000 1, -0.000000, -0.000000, 0.000000, -1.716660, -98.357374, 81.642621 2, 0.000001, -3.200000, 3.200000, -1.570796, -89.999988, -89.999988 3, -0.000000, 0.000000, 0.000000, 1.652756, 94.695926, -85.304069 |
sin(2x)의 절반 파형만 도배!
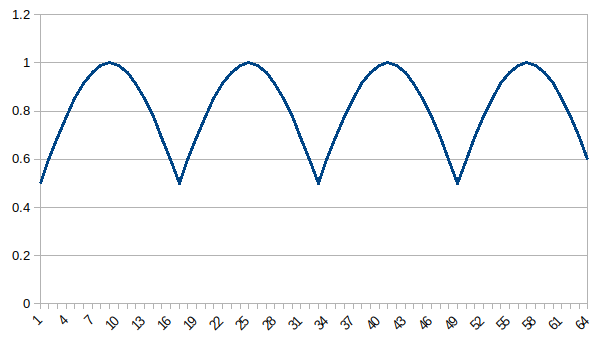
고조파 처럼 나오네?
DC 52.3
4Hz 6.8, 8Hz 1.42, 12Hz 0.65, 16Hz 0.39, 20Hz 0.28, 24Hz 0.23, 28Hz0.20, 32Hz 0.19 (합계 10.251662)
| Output FFT Coefficients: 0, 52.306340, 0.000000, 52.306340, 0.000000, 0.000000, 0.000000 1, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 2, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 3, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 4, -6.856612, -0.000001, 6.856612, -3.141593, -179.999990, 0.000005 5, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 6, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 7, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 8, -1.425690, -0.000000, 1.425690, -3.141592, -179.999986, 0.000009 9, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 10, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 11, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 12, -0.652365, -0.000000, 0.652365, -3.141592, -179.999983, 0.000012 13, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 14, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 15, 0.000000, 0.000000, 0.000000, 0.000000, 0.000000, -nan 16, -0.397825, -0.000000, 0.397825, -3.141592, -179.999982, 0.000013 17, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 18, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 19, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 20, -0.286168, -0.000000, 0.286168, -3.141592, -179.999983, 0.000012 21, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 22, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 23, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 24, -0.231164, -0.000000, 0.231164, -3.141592, -179.999986, 0.000009 25, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 26, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 27, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 28, -0.204855, -0.000000, 0.204855, -3.141593, -179.999990, 0.000005 29, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 30, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 31, 0.000000, -0.000000, 0.000000, -0.000000, -0.000000, -nan 32, -0.196983, 0.000000, 0.196983, 3.141593, 179.999995, -0.000000 |
'프로그램 사용 > fft, fftw' 카테고리의 다른 글
| overlap kissfft (0) | 2023.06.12 |
|---|---|
| fft size overlap window size (0) | 2023.06.12 |
| fft 잘못 사용하고 있었나? (0) | 2023.06.02 |
| fft 라이브러리 목록 (0) | 2023.06.01 |
| fftw 다차원 분석 (0) | 2023.05.27 |

